April 10, 2018, 4:45-7pm:
  • Facilitators: Karin Lange and Emily Peters
  • Topic: TBA

    • Feb 6, 2018, 4:45-7pm:
  • Facilitators: Amanda Harsy (Lewis University) and Rita Patel (College of DuPage)
  • Topic: Liar's Bingo

    • Dec. 5, 2017, 4:45-7pm:
  • Facilitators: Brian Seguin and Peter Tingley
  • Topic: NIM and other related games.

    • Oct. 3, 2017, 4:45-7pm:

  • Facilitators: Peter Tingley
  • Topic: Problem solving!
    • It has been three years since we really exlained what our math circle is about, and most of you weren't at that session. Also, our opinions have evolved. So we are going have another go at introducing problem solving! But don't worry, I'm going to use all new problems, so if you were at the previous session it should seem completely different.
    April 4, 2017
  • Facilitators: Peter Tingley
  • Topic: Controlling growth. Or is it growth controlling you?

    • I enjoyed this so much, I celebrated by writing a full lesson plan! If you would like to see, it is here. Note: this version is intended for outreach with pretty bright and enthusiastic high school students.

    Feb 7, 2017
  • Facilitators: Steve Jordan (Loyola)
  • Topic: What makes a circle a circle?

    • There seems to have been some sort of slide show at this session. It is here.

    Dec 6, 2017
    Facilitators: Peter Tingley and Adriano Zambom.
    Topic: Perilous Probability
    We discussed the Monte Hall problem. Then we worked on the question:
    Oct 4, 2017
    Taxicab geometry Facilitator: Yvonne Lai (U. of Nebraska, Lincoln).
    The idea of distance seems pretty straightforward, but sometimes the usual definition isn't actually what you want. For instance, if you are driving a taxi around a grid of city streets, you don't actually care about the straight line distance between points, but instead you c are about how far you need to drive to get from one to the other. This is a new and different notion of distance, and you can use it to build up a new and different idea of w hat geometry should be. We will explore that, asking questions like, what is a line in this geometry? What is a circle? How about a parabola?

    Here are links to some stuff we used in this session:

    Beginning to draw an ellipse

    Ellipse drawing animation

    Desmos link (created by Erin Baldinger)

    The game SET, and some geometry (5/3/2016). Facilitators: Anne Agostinelli and Casey McLeod

    Voting systems (3/29/2016). Facilitator: Peter Tingley
    Mostly taken from here.

    The watermelon problem (1/26/2016). Facilitator: Peter Tingley
    How many pieces can you cut a watermelon into using 10 cuts?
  • This was intended to mean the most pieces possible.
  • It is most interesting if you assume the watermelon pieces don't move between cuts (so it all stays ogether as you cut it 10 times, then you take it all apart).
  • The hint here is: find simpler versions of the problem...but maybe not the most obvious simpler version.
  • If you want to have more fun, try doing this with a donute instead of a watermelon.


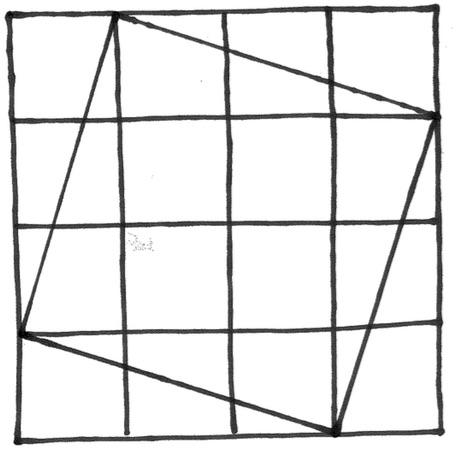
    • Counting squares (12/1/2015). Facilitator: Peter Tingley
  • How many squares are there in a ten by ten piece of graph paper?

    • This only becomes interesting when you allow squares that are bigger than 1 by 1. It became really interesting when we allowed squares that were crooked, like the one shown below. That is, squares where the corners are at corners of the graph paper, but the edges do not need to follow the edges.



    The princess problem (9/29/2015)

    Bluffing at poker (9/29/2015). Facilitator: Peter Tingley
  • Is bluffing a good idea in poker? Somewhat more precisely, assuming the other player knows your strategy (but not your hand), is it a good idea to use a strategy that involves bluffing?

    • Perhaps surprisingly, the answer is an unequivocal yes! You should sometimes bluff, even against a player who knows your strategy and plays perfectly. To work this out, we considered the following simplified game:

  • Each player's "hand" is determined by the role of a die.
  • There is no drawing, etc.
  • Betting is as follows: each player antes $1. Then player 1 may either bet $1, or pass. If player 1 bet, player 2 can either call by putting in $1, or fold. If player 1 passed, there is no more betting.
  • If player 2 folded, player 1 gets the pot. Otherwise,the players compare hands; the higher hand gets the pot or, if there is a tie, the players split the pot.

    • Frogs and toads (03/31/2015). Facilitator: Peter Tingley
    This problem comes from the summer 2013 issue summer 2013 issue of MTCircular, the magazine of the Math Teachers' Circle Network.

  • Frogs and toads are arranged on a 5 by 5 board as shown below. They would like to switch places. That is, they want to move so that in the end there is a frog on each square where there was a toad, and vise-versa. Frogs can move one space right or down, and Toads can move one space left or up. They can also jump over exactly one of the other kind of animal (in a direction they are allowed to go) to land in an empty space. Can this be done? How long will it take? ...




    • Picture from our inaugural session: